Quantum Tic-Tac-Toe

경고: 아직 완성되지 않은 게시글입니다.

Intro

지금까지는 우리가 사는 세상을 물리학적으로 두 가지로 구분할 수 있는데, 하나는 우리가 일상에서 쉽게 접하고 접촉을 할 수 있는 ‘고전적인(Classical)’ 세상과, 일반 사람의 눈으로 관찰조차 힘든, 매우 미시적인 세계인 ‘양자(Quantum)’ 세상으로 나눌 수 있다. 이 양자 세계에서는 관측 조차 힘들 뿐더러 관측하는 행위 조차 계에 영향을 끼치는 등, 도통 일반 사람들이 이해하기 어려운 모습들이 보인다.

이러한 Quantum System에서 나타나는 현상을 ‘고전적인 대응물(Classical counterpart)’¹에 설명을 하려는 여러가지 시도가 있다. 예를 들면 전자의 스핀현상을 구의 형태의 회전으로 생각하고 설명을 하는 등이 있다. 이렇게 양자적 현상을 설명하는 방법 중, 게임을 이용하여 설명하려는 방법이 있다. 이 게시글에서는 Tic-Tac-Toe 게임에 양자적 현상을 접목시킨 Quantum Tic-Tac-Toe에 대해 소개하려고 한다. 이 게시글에 대한 설명이 부족하다고 생각되면 Wikipedia를 참고하면 된다.

Wikipedia Post 이동하기

잠깐… Tic-Tac-Toe는 뭘까요?

Tic-Tac-Toe는 간단하게 말해 ‘오목’ ‘빙고’ 비슷한 것이라고 보면 된다. 물론 이들 게임보다는 재미가 없다. 이 게임에 대한 룰을 써보면,

• 두 명이서 플레이
• 3x3의 칸으로 이루어진 판에서 번갈아가며 마킹
• 먼저 자신의 말로 한 줄을 만들어 내는 사람이 승리

너무나 간단해서 오목이나 빙고보다 재미가 없을 수 밖에 없다!! 하지만, 이렇게 간단하기 때문에 양자현상을 접목시키기 더 편리하다. 기존 게임이 복잡할 수록 고려해야 할 것이 너무 많기 때문이다.

Tic-Tac-Toe 게임의 예시. Player O가 한줄을 먼저 만들었기 때문에 승리했다.

Quantum Tic-Tac-Toe의 게임방식

Tic-Tac-Toe의 양자현상을 접목시킨 Quantum Tic-Tac-Toe는 Classical Tic-Tac-Toe²의 Rule을 포함하고, 여기서 양자 현상을 게임에 접목시킨 새로운 Rule을 추가한다. 추가된 Rule은 다음과 같다.

• 플레이어는 자기차례가 되면 동일한 칸을 제외한 두 개의 칸에 마킹
• 특정 상황이 되면 플레이어가 놓은 위치를 상대 플레이어가 선택
• 상대 플레이어가 선택하고 나면, 기존의 Tic-Tac-Toe로 돌아감
• 기존의 Tic-Tac-Toe 상황에서 한 줄을 먼저 만들어낸 플레이가 승리

일단 한 플레이어가 하나를 마킹하던 것을 두 개 마킹함으로 복잡해졌다. 그만큼 제한조건이 생겼는데, 바로 2번째 특정상황. 이것에 대해서는 게임방법을 살펴보면서 알아보도록 하자.

Quantum Tic-Tac-Toe의 게임방법

1. 기존의 Tic-Tac-Toe 규칙을 그대로 적용

우리가 Quantum System을 관측하게 되면 곧바로 기존의 Classical System으로 붕괴하는 것이 된다. 또한 Quantum System은 Classical System으로 회귀하는 대응원리가 있으므로 이 규칙을 그대로 적용한다. 다만 다음 항목부터는 양자계에서 일어난다고 가정하고 서술한다.

2. Player는 자기차례일 때 동일한 칸을 제외한 두 개의 칸에 마킹

앞에서 설명한 것으로, 두 개의 칸에 마킹을 할 수 있지만, 동일한 칸에는 마킹하는 것이 불가능 하다. 이는 그렇게 하면 게임이 재미 없고, 또 동일한 칸에 마킹을 한다는 것은 결국 고전적으로 마킹한 것이나 다름이 없다. 보다 수학적으로 서술하면, Player Alice가 처음 시도한 횟수를

\[\begin{align} \vert {T_1}\rangle_{A} = \frac{1}{\sqrt{2}}(\vert T_{11}\rangle + \vert T_{12}\rangle) \end{align}\]

이라고 할 수 있다. 그런데 여기서 같은 칸에 마킹을 한다는 것은,

\[\begin{align} \vert T_1\rangle_{A} & = \frac{1}{\sqrt{2}}(\vert T_{11}\rangle + \vert T_{11}\rangle) \\ & = \vert T_{11}\rangle \end{align}\]

이 되는 것으므로 결국 1의 확률로 확정적으로 마킹한 칸에 있게 되는 것이다. 고전적인 Tic-Tac-Toe와 다른 것이 없다.

Quantum Tic-Tac-Toe의 예제.

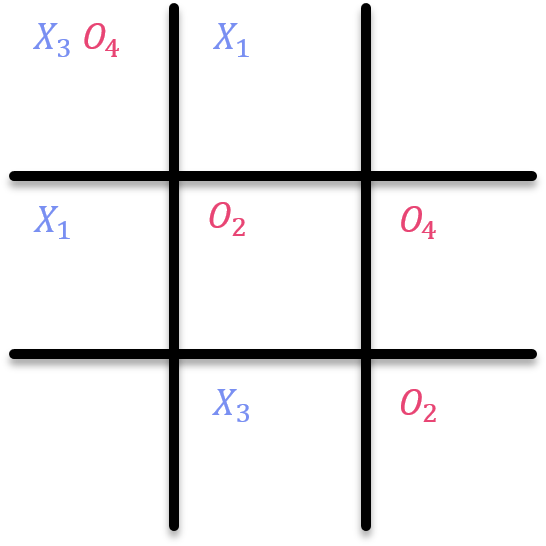
3. Cyclic Entanglement

이 현상은 두 플레이어가 게임을 하고 있는 도중에 나타나는 현상이다. 다음의 예시를 살펴보도록 하자.

예제에서 Cyclic Entanglement가 형성이 된 모습.

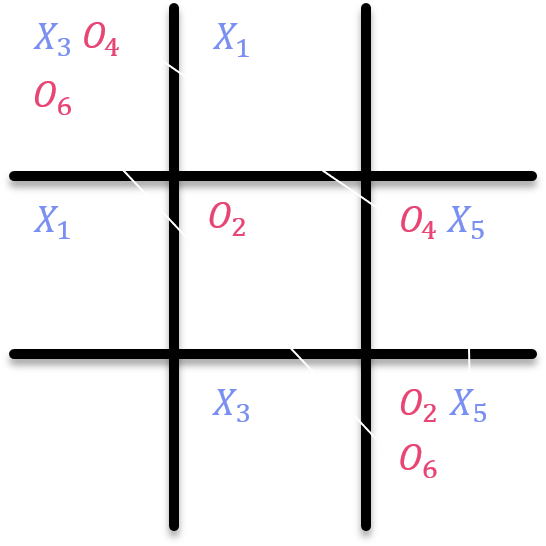
그림을 살펴보면 Player O가 6번째 ($O_{6}$)에 놓은 상황에서, 하나의 Cycle이 형성되는 것을 확인할 수 있는데, 하나씩 순서를 살펴보면,

\[\begin{align} {O_{6}}_{(1,1)} \rightarrow {O_{6}}_{(3,3)} \rightarrow {X_{5}}_{(1,1)} \rightarrow {X_{5}}_{(2,3)} \rightarrow {O_{4}}_{(2,3)} \\ \rightarrow {O_{4}}_{(1,1)} \rightarrow {O_{6}}_{(1,1)} \nonumber \end{align}\]

와 같이 순환 고리가 형성이 된다. 이를 Cyclic Entanglement 라고 부른다. 이 때 상대 Player X는 이 Cycle을 붕괴(Collapse) 해주어야 한다. 이 상황을 붕괴 시키는 방법은 Player O가 최종적으로 놓았던 위치,

\[\begin{align} {O_{6}}_{(1,1)} \qquad {O_{6}}_{(3,3)} \end{align}\]

둘 중에 $O_{6}$를 측정할 위치를 선택해야 한다.

4. Collapse

Player X는 ${O_{6}}$가 중첩된 위치 (1,1)과 (3,3)에 대하여 선택을 해야한다.

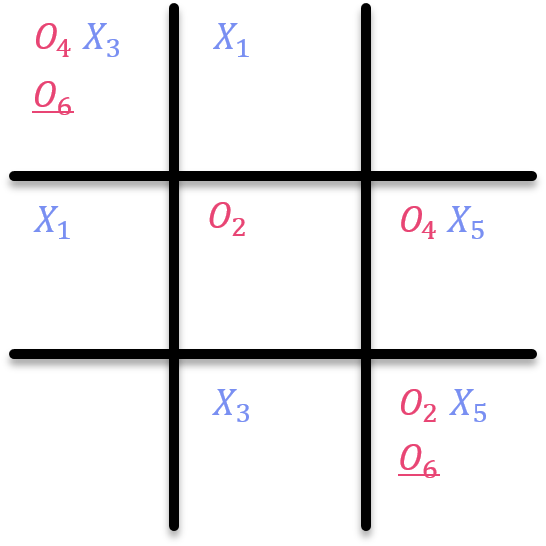
Case 1. ${O_{6}}_{(1,1)}$ 을 선택하는 경우

Player X가 (1,1)에 위치한 ${O_{6}}$를 선택하면, Collapse가 발생한 뒤 아래와 같이 Classical Tic-Tac-Toe 상태로 돌아가게 된다.

(1,1)에 위치한 O6를 선택했을 때 발생한 붕괴상태

하나씩 순서를 살펴보도록 하자.

---

1. ${O_{6}}_{(1,1)}$을 선택했기 때문에, 이 자리에는 반드시 $O_6$가 있어야 한다.
2. 따라서 같은 자리에 있는 ${O_4}_{(1,1)}$, ${X_3}_{(1,1)}$는 다른 자리에 중첩되어 있는 ${O_4}_{(2,3)}$, ${X_3}_{(3,2)}$ 에 존재하게 된다.
3. 이 때 ${X_3}_{(3,2)}$는 다른 종속된 변수들이 없기 때문에, 충돌하는 것이 없지만, ${O_4}_{(2,3)}$은 ${X_5}_{(2,3)}$과 충돌한다. 이 경우에는, ${O_4}_{(2,3)}$가 자리를 차지하게 된다. 그럴 수 밖에 없는데, 이는 \(\begin{align} \vert T_{4}\rangle_O = \frac{1}{\sqrt{2}}({\vert T_{4}\rangle_{O}}_{(1,1)} + {\vert T_{4}\rangle_{O}}_{(2,3)}) \end{align}\) 이고 Player X가 측정을 할 때 ${O_6}_{(1,1)}$를 선택하였기 때문에, 고전적인 상황에서는 반드시 ${O_4}_{(2,3)}$가 모습을 드러내야 한다. 이는 Entanglement 현상 때문이다.
4. 한편 ${X_5}$는 (2,3)과 (3,3)으로 중첩되어 있으며 역시 Entanglement 때문에 (3,3)이 발현되어야 한다. 같은 자리에 있는 ${O_6}_{(2,3)}$ 는 이미 (1,1)에서 측정하였기에 Classical 상황에서는 나타나지 않으며, 따라서 ${O_2}_{(3,3)}$를 고려해주어야 하는데, 이 때 ${X_5}$가 발현되기 때문에 역시 ${O_2}_{(3,3)}$가 측정되는 확률은 낮다.
5. ${O_2}$는 (3,3)과 (2,2)에 중첩되어 있다. (2,2)에 위치한 ${O_2}$는 어떠한 것과도 연관되어 있지 않으므로 (2,2)에는 O로 측정이 된다.
6. 한편 ${X_1}$의 경우에는 (1,2), (2,1)에 위치하고 있는 데, 이들 성분은 서로 중첩 그리고 얽혀있을 뿐 다른 Player나 시도(Trial)와는 연결되어 있지 않다. 따라서 Measurement가 이루어지더라도, Quantum State를 유지한다.

---

Case 2. ${O_6}_{(3,3)}$ 을 선택하는 경우

Player X가 (3,3)에 위치한 ${O_6}$를 선택하면, Collapse가 발생한 뒤 아래와 같이 Classical Tic-Tac-Toe 상태로 돌아가게 된다.

(3,3)에 위치한 O6를 선택했을 때 발생한 붕괴상태

놀랍게도 Case 1과 다르게 O가 한 줄을 만들어 내어 승리했다! 순서를 살펴보도록 하자.

---

1. ${O_6}_{(3,3)}$을 선택했기 때문에, 이 자리에는 반드시 $O_6$가 있어야 한다.
2. 따라서 같은 자리에 있는 ${O_2}_{(3,3)}$, ${X_5}_{(3,3)}$은 다른 자리에 중첩되어 있는 ${O_2}_{(2,2)}$, ${X_5}_{(2,3)}$에 존재하게 된다.
3. ${O_2}_{(2,2)}$에는 어떠한 것과도 관련이 없으므로, Classical로 돌아가면 O로 측정된다.
4. 한편 (2,3)에는 ${X_5}_{(2,3)}$, ${O_4}_{(2,3)}$이 존재한다. 이 때 측정되는 것은 $X_5$ 인데, 앞의 경우와 같이 \(\begin{align} |T_{5}\rangle_X = \frac{1}{\sqrt{2}}({|T_{5}\rangle_X}_{(2,3)} + {|T_{5}\rangle_X}_{(3,3)}) \end{align}\) 이고 Player X가 측정할 때 ${O_6}_{(3,3)}$을 측정하였으므로 고전적인 상황에서는 반드시 ${X_5}_{(2,3)}$가 모습을 드러내야 한다.
5. 마찬가지로 $O_4$는 (1,1)에서 측정이 되고, 자연스레 ${X_3}_{(1,1)}$는 측정되지 않고 (3,2)에 있는 ${X_3}_{(2,3)}$이 모습을 드러낸다.
6. 한편 Case 1과 같이 ${X_1}$은 어떠한 것과도 얽혀있지 않기 때문에 Quantum State를 유지한다.

---

Quantum Tic-Tac-Toe에서 발생할 수 있는 상황

• 측정 후 동시에 서로 한 줄을 만들었을 때

References

• Goff, Allan; Lehmann, Dale; Siegel, Joel (2002-07-07). “Quantum Tic-Tac-Toe, Spooky-Coins & Magic-Envelopes, as Metaphors for Relativistic Quantum Physics”
• Wikipedia Quantum Tic-Tac-Toe

1. 여기서 이러한 단어를 굳이 언급하는 이유는, 양자계를 반드시 고전적인 계와 구분할 필요가 있기 때문이다. 일부 사람들은 이러한 계를 구분하지 않고 양자역학을 잘못 이해하는 사람이 너무 많다. 대표적인 예를 든다면 ‘슈뢰딩거 고양이’현상을 아무 생각없이 현실적으로 (고전적인 계에서)일어난다고 보고 그대로 대입하는… 어처구니 없는 행동이 있다. ↩

2. 앞으로는 기존의 Tic-Tac-Toe를 ‘고전적인(Classical) Tic-Tac-Toe’라고 지칭을 하겠다. 물리학에서는 양자계 이전까지의 계를 ‘고전적(Classical)’ 이라고 지칭하기 때문에 이쪽 용어를 쓰는 것이 더 편리하다. ↩